
Summary
| 2D | 3D |
|---|---|
 Triángulo truncado o hexágono uniforme, con diagrama de Coxeter-Dynkin |
 Octaedro truncado |
| 4D | 5D |
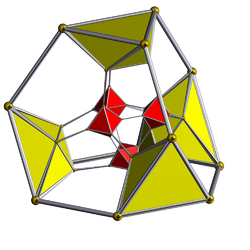 16-celdas truncado |
 5-ortoplex truncado |
En geometría, un politopo uniforme de dimensión tres o superior es una forma geométrica isogonal delimitada por facetas uniformes. Los politopos uniformes en dos dimensiones son los polígonos regulares (la definición es diferente en 2 dimensiones, para excluir a los polígonos de lados pares vértice-transitivos que alternan dos longitudes diferentes de aristas).
Esta es una generalización de la categoría anterior de politopos semirregulares, pero también incluye los politopos regulares. Además, se permiten tanto caras regulares como figuras de vértice con forma de estrella (polígonos estrellados), lo que amplía enormemente las posibles soluciones. Una definición estricta requiere que los politopos uniformes sean finitos, mientras que una definición más amplia permite que los panales uniformes (teselados bidimensionales y panales de dimensiones superiores) de los espacios euclídeo e hiperbólico también se consideren politopos.[1]
Operaciones
editarCasi todos los politopos uniformes pueden generarse a partir de una construcción de Wythoff y representarse mediante un diagrama de Coxeter-Dynkin. Excepciones notables son el gran dirrombicosidodecaedro en tres dimensiones y el gran antiprisma en cuatro dimensiones. La terminología para los politopos uniformes convexos (utilizada en los artículos poliedro uniforme, 4-politopo uniforme, 5-politopo uniforme, 6-politopo uniforme, teselado uniforme y panal convexo uniforme) fue acuñada por Norman Johnson.
De manera equivalente, los politopos wythoffianos se pueden generar aplicando operaciones básicas a los politopos regulares en estas dimensiones. Este enfoque fue utilizado por primera vez por Johannes Kepler, y es la base de la notación de poliedros de Conway.
Operadores de rectificación
editarLos n-politopos regulares tienen n órdenes de rectificación. La rectificación cero es la forma original. La (n−1)-ésima rectificación es el poliedro conjugado. Una rectificación reduce las aristas a vértices, una birrectificación reduce las caras a vértices, una trirrectificación reduce las celdas a vértices, una cuatrirrectificación reduce las 4-caras a vértices, una quintirrectificación reduce las 5-caras a vértices, y así sucesivamente.
Se puede utilizar un símbolo de Schläfli extendido para representar formas rectificadas, con un solo subíndice:
- k-ésima rectificación = tk{p1, p2, ..., pn-1} = kr.
Operadores de truncamiento
editarLas operaciones de truncamiento se pueden aplicar a n-politopos regulares en cualquier combinación. El diagrama de Coxeter resultante tiene dos nodos anillados y la operación recibe el nombre de la distancia entre ellos. El truncamiento corta vértices, el canteado' corta aristas, la runcinación corta caras, y la estericación corta celdas. Cada operación superior también abarca a las inferiores, de modo que (por ejemplo), un canteado también trunca vértices.
- t0,1 o t: Truncamiento: se aplica a polígonos y a figuras de dimensiones superiores. Un truncamiento elimina los vértices e inserta una nueva faceta en lugar de cada unos de los vértices anteriores. Las caras se truncan, duplicando su número de aristas (el término, acuñado por Johannes Kepler, proviene del latín truncare, "cortar".)
- También hay truncamientos superiores: bitruncamiento t1,2 o 2t, tritruncamiento t2,3 o 3t, cuatritruncamiento t3,4 o 4t, quintitruncamiento t4,5 o 5t, etc.
- t0,2 o rr: Canteado: se aplica a poliedros y a figuras de dimensiones superiores. Puede verse como una rectificación de una primera rectificación. Un canteado trunca tanto los vértices como las aristas y los reemplaza por nuevas facetas. Las células son reemplazadas por copias topológicamente expandidas de sí mismas (el término, acuñado por Johnson, se deriva del verbo cant, como biselar", que significa cortar según un plano inclinado).
- También hay canteados superiores: bicanteado t1,3 o r2r, tricanteado t2,4 o r3r, cuatricanteado t3,5 o r4r, etc.
- t0,1,2 o tr: Cantitruncamiento: se aplicada a poliedros y a figuras de dimensiones superiores. Se puede considerar que trunca una forma rectificada. Un cantitruncamiento secciona tanto los vértices como las aristas, y los reemplaza por nuevas facetas. Las células son reemplazadas por copias topológicamente expandidas de sí mismas (el término compuesto combina canteado y truncamiento)
- También hay cantitruncamientos superiores: bicantitruncamiento t1,2,3 o t2r, tricantitruncamiento t2,3,4 o t3r, cuatricantitruncamiento t3,4,5 o t4r, etc.
- t0,3: Runcinado: se aplica a 4-politopos uniformes y a figuras de dimensiones superiores. El runcinado trunca vértices, aristas y facetas, reemplazándolos a cada uno por nuevas facetas. Las 4-facetas son reemplazadas por copias topológicamente expandidas de sí mismas (el término, acuñado por Johnson, se deriva del latín runcina, la "garlopa" usada por los carpinteros).
- También hay runcinados superiores: birruncinado t1,4, trirruncinado t2,5, etc.
- t0,4 o 2r2r: Estericación: se aplica a 5-politopos uniformes y figuras de dimensiones superiores. Puede verse como una birrectificación de una birrectificación. La estericación trunca vértices, aristas, caras y celdas, reemplazando cada uno por nuevas facetas. Las 5-caras son reemplazadas por copias topológicamente expandidas de sí mismas (el término, acuñado por Johnson, se deriva del griego estéreo, "sólido".)
- También hay estericaciones superiores: biestericación t1,5 o 2r3r, triestericación t2,6 o 2r4r , etc.
- t0,2,4 o 2t2r: Estericanteado: se aplica a 5-politopos uniformes y a figuras de dimensiones superiores. Puede verse como el bitruncamiento de una birrectificación.
- También hay estericanteados superiores: biestericanteado' t1,3,5 o 2t3r, tristericanteado t2,4,6 o 2t4r, etc.
- t0,5: Pentelación: se aplica a 6-politopos uniformes y a figuras de dimensiones superiores. La pentelación trunca vértices, aristas, caras, celdas y 4-caras, reemplazando cada uno por nuevas facetas. Las 6-caras son reemplazadas por copias topológicamente expandidas de sí mismas(el término pentelación deriva del prefijo griego pente, "cinco").
- También hay pentelaciones superiores: bipentelación t1,6, tripentelacion t2,7, etc.
- t0,6 o 3r3r: Hexilación: se aplica a 7-politopos uniformes y a figuras de dimensiones superiores. Puede verse como una trirectificación de una trirectificación. La hexilación trunca vértices, aristas, caras, celdas, 4-caras y 5-caras, reemplazando cada uno por nuevas facetas. Las 7-caras son reemplazadas por copias topológicamente expandidas de sí mismas (el término hexilación deriva del griego hex, "seis").
- También hay hexilaciones superiores: bihexilación': t1,7 o 3r4r, trihexilación: t2,8 o '3r5r, etc.
- t0,3,6 o 3t3r: Hexiruncinado: se aplica a 7-politopos uniformes y a figuras de dimensiones superiores. Puede verse como un tritruncamiento de una trirectificación.
- También hay hexiruncinaciones superiores: bihexiruncinado: t1,4,7 o 3t4r, trihexiruncinado: t2,5,8 o 3t5r, etc.
- t0,7: Heptelación: se aplica a 8-politopos uniformes y a figuras de dimensiones superiores. La heptelación trunca vértices, aristas, caras, celdas, 4 caras, 5-caras y 6-caras, reemplazando cada una por nuevas facetas. Las 8-caras son reemplazadas por copias topológicamente expandidas de sí mismas (el término heptelación deriva del griego hepta, "siete").
- También hay heptelaciones superiores: biheptelación t1,8, triheptelación t2,9, etc.
- t0,8 o 4r4r: Octelación: se aplica a 9-politopos uniformes y a figuras de dimensiones superiores.
- t0,9: Enelación: se aplica a 10-politopos uniformes y a figuras de dimensiones superiores.
Además, se pueden realizar combinaciones de truncamientos que también generan nuevos politopos uniformes. Por ejemplo, un runcitruncamiento es una runcinación y un truncamiento aplicados juntos.
Si se aplican todos los truncamientos a la vez, la operación puede denominarse de manera más general como omnitruncado.
Alternación
editar
Una operación especial, llamada alternación, elimina vértices alternativos de un politopo que solo tiene caras pares. Un politopo omnitruncado alternado se llama romo.
Los politopos resultantes siempre se pueden construir, y generalmente no son reflectantes y, en general, tampoco tienen soluciones de politopos uniformes.
El conjunto de politopos formados alternando un hipercubo se conocen como demicubos. En tres dimensiones, esta operación produce un tetraedro; en cuatro dimensiones, se genera un 16-celdas, o demiteseracto.
Figura de vértice
editarSe pueden construir politopos uniformes a partir de su figura de vértice, la disposición de aristas, caras, celdas, u otros elementos de dimensiones superiores alrededor de cada vértice. Los politopos uniformes representados por un diagrama de Coxeter-Dynkin, que marcan espejos activos mediante anillos, tienen simetría reflexiva y pueden construirse simplemente a partir de reflexiones recursivas de la figura del vértice.
Un número menor de politopos uniformes no reflexivos tienen una única figura de vértice, pero que no se repite mediante reflexiones simples. La mayoría de estos cuerpos se pueden representar con operaciones como la alternación de otros politopos uniformes.
Las figuras de vértice para diagramas de Coxeter de anillo único se pueden construir a partir del diagrama, eliminando el nodo anillado y anillando los nodos vecinos. Estas figuras de vértice son en sí mismas vértice-transitivas.
Los politopos de anillos múltiples se pueden generar empleando un proceso de construcción un poco más complicado y su topología no es un politopo uniforme. Por ejemplo, la figura del vértice de un politopo regular truncado (con 2 anillos) es una pirámide. Un politopo omnitruncado (todos los nodos anillados) siempre tendrá un símplex irregular como figura de vértice.
Circunradio
editarLos politopos uniformes tienen aristas de igual longitud y todos los vértices están a la misma distancia del centro, lo que se denomina circunradio.
Los politopos uniformes cuyo circunradio es igual a la longitud de las aristas se pueden utilizar como figura de vértice para los panales uniformes. Por ejemplo, el hexágono regular se divide en 6 triángulos equiláteros y es la figura de vértice del teselado triangular regular. Además, el cuboctaedro se divide en 8 tetraedros regulares y 6 pirámides cuadradas (la mitad del octaedro), y es la figura del vértice del panal cúbico alternado.
Politopos uniformes por dimensión
editarEs útil clasificar los politopos uniformes por su dimensión, que equivale al número de nodos en el diagrama de Coxeter, o al número de hiperplanos en la construcción Wythoffiana. Debido a que los politopos de (n+1) dimensiones son teselados del espacio esférico de n dimensiones, los teselados euclídeos e hiperbólicos de n dimensiones también se consideran (n+ 1)-dimensionales. Por tanto, los teselados del espacio bidimensional se agrupan con los sólidos tridimensionales.
Una dimensión
editarEl único politopo unidimensional es el segmento de recta. Corresponde a la familia de Coxeter A1.
Dos dimensiones
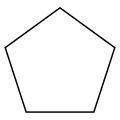
editarEn dos dimensiones, existe una familia infinita de politopos uniformes convexos, los polígonos regulares, siendo el más simple el triángulo equilátero. Los polígonos regulares truncados se convierten geométricamente en polígonos cuasirregulares bicolores del doble de lados, t{p}={2p}. Los primeros polígonos regulares (y formas cuasirregulares) se muestran a continuación:
| Nombre | Triángulo (2-símplex) |
Cuadrado (2-ortoplex) (2-cubo) |
Pentágono | Hexágono | Heptágono | Octógono | Eneágono | Decágono | Endecágono |
|---|---|---|---|---|---|---|---|---|---|
| Schläfli | {3} | {4} t{2} |
{5} | {6} t{3} |
{7} | {8} t{4} |
{9} | {10} t{5} |
{11} |
| Diagrama de Coxeter |
|||||||||
| Imagen | 
|
 
|
|
 
|

|
 
|

|
 
|

|
| Nombre | Dodecágono | Tridecágono | Tetradecágono | Pentadecágono | Hexadecágono | Heptadecágono | Octodecágono | Polígono | Isodecágono |
| Schläfli | {12} t{6} |
{13} | {14} t{7} |
{15} | {16} t{8} |
{17} | {18} t{9} |
{19} | {20} t{10} |
| Diagrama de Coxeter |
|||||||||
| Imagen |  
|

|
|

|
 
|

|
 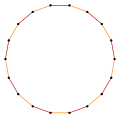
|

|
 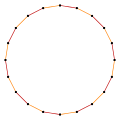
|
También hay un conjunto infinito de estrellas (una por cada número racional mayor que 2), pero no son convexas. El ejemplo más sencillo es la estrella pentagonal, que corresponde al número racional 5/2. Los polígonos de estrellas regulares, {p/q}, se pueden truncar en polígonos de estrellas semirregulares, t{p/q}=t{2p/q}, pero se convierten en recubrimientos dobles si q es par. También se puede realizar un truncamiento con un polígono de orientación inversa t{p/(p-q)}={2p/(p-q)}, por ejemplo t{5/3}={10/3}.
| Nombre | Estrella pentagonal | Heptagramas | Octagrama | Eneagramas | Decagrama | ...n-agramas | ||
|---|---|---|---|---|---|---|---|---|
| Schläfli | {5/2} | {7/2} | {7/3} | {8/3} t{4/3} |
{9/2} | {9/4} | {10/3} t{5/3} |
{p/q} |
| Diagrama de Coxeter |
||||||||
| Imagen | 
|

|

|
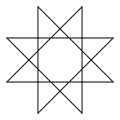 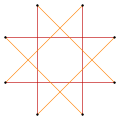
|

|

|
|
|
Polígonos regulares, representados por Símbolo de Schläfli {p} para un p-gon. Los polígonos regulares son autoduales, por lo que la rectificación produce el mismo polígono. La operación de truncamiento uniforme duplica los lados a {2p}. La operación de desaire, alternando el truncamiento, restaura el polígono original {p}. Por tanto, todos los polígonos uniformes también son regulares. Se pueden realizar las siguientes operaciones en polígonos regulares para derivar polígonos uniformes, que también son polígonos regulares:
| Operación | Símbolos de Schläfli extendidos |
Resultado regular |
Diagrama de Coxeter |
Posición | Simetría | ||
|---|---|---|---|---|---|---|---|
| (1) | (0) | ||||||
| Original | {p} | t0{p} | {p} | {} | -- | [p] (orden 2p) | |
| Rectificado (Dual) |
r{p} | t1{p} | {p} | -- | {} | [p] (orden 2p) | |
| Truncado | t{p} | t0,1{p} | {2p} | {} | {} | [[p]]=[2p] (orden 4p) | |
| Mitad | h{2p} | {p} | -- | -- | [1+,2p]=[p] (orden 2p) | ||
| Achatado | s{p} | {p} | -- | -- | [[p]]+=[p] (orden 2p) | ||
Tres dimensiones
editarEn tres dimensiones se incrementa la variedad de formas. Hay cinco poliedros regulares convexos, conocidos como sólidos platónicos:
| Nombre | Schläfli {p,q} |
Diagrama |
Imagen (transparente) |
Imagen (sólida) |
Imagen (esférica) |
Caras {p} |
Aristas | Vértices {q} |
Simetría | Dual |
|---|---|---|---|---|---|---|---|---|---|---|
| Tetraedro (3-símplex) (Pirámide) |
{3,3} | 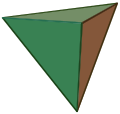
|

|

|
4 {3} |
6 | 4 {3} |
Td | (autodual) | |
| Cubo (3-cubo) (Hexaedro) |
{4,3} | 
|

|

|
6 {4} |
12 | 8 {3} |
Oh | Octaedro | |
| Octaedro (3-ortoplex) |
{3,4} | 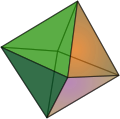
|

|

|
8 {3} |
12 | 6 {4} |
Oh | Cubo | |
| Dodecaedro | {5,3} | 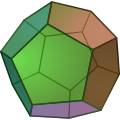
|

|

|
12 {5} |
30 | 20 {3}2 |
Ih | Icosaedro | |
| Icosaedro | {3,5} | 
|

|

|
20 {3} |
30 | 12 {5} |
Ih | Dodecaedro |
También hay 13 poliedros semirregulares, o sólidos arquimedianos, que se pueden obtener mediante la construcción de Wythoff o realizando operaciones en los sólidos platónicos, tal como se muestra en la siguiente tabla:
| Original | Truncado | Rectificado | Bitruncado (dual truncado) |
Birrectificado (dual) |
Canteado | Omnitruncado (Cantitruncado) |
Romo | |
|---|---|---|---|---|---|---|---|---|
| Tetraédrica 3-3-2 |
 {3,3} |
 (3.6.6) |
 (3.3.3.3) |
 (3.6.6) |
 {3,3} |
 (3.4.3.4) |
 (4.6.6) |
 (3.3.3.3.3) |
| Octaédrica 4-3-2 |
 {4,3} |
 (3.8.8) |
 (3.4.3.4) |
 (4.6.6) |
 {3,4} |
 (3.4.4.4) |
 (4.6.8) |
 (3.3.3.3.4) |
| Icosaédrica 5-3-2 |
 {5,3} |
 (3.10.10) |
 (3.5.3.5) |
 (5.6.6) |
 {3,5} |
 (3.4.5.4) |
 (4.6.10) |
 (3.3.3.3.5) |
También existe un conjunto infinito de prismas, uno para cada polígono regular, y un conjunto correspondiente de antiprismas.
| # | Nombre | Imagen | Teselado | Figura de vértice |
Diagrama y símbolo de Schläfli |
|---|---|---|---|---|---|
| P2p | Prismas | 
|

|

|
tr{2,p} |
| Ap | Antiprismas | 
|

|

|
sr{2,p} |
Los poliedros estelares uniformes incluyen otros 4 poliedros estelares regulares, el sólido de Kepler-Poinsot, y 53 poliedros estelados semirregulares. También hay dos conjuntos infinitos, los prismas estelares (uno por cada polígono estelar) y los antiprismas estelares (uno por cada número racional mayor que 3/2).
Construcciones
editarLos poliedros y mosaicos uniformes de Wythoff se pueden definir por su símbolo de Wythoff, que especifica el dominio fundamental del objeto. Una extensión de la notación de Schläfli, también utilizada por Coxeter, se aplica a todas las dimensiones. Consta de la letra 't', seguida de una serie de números con subíndices correspondientes a los nodos anillados del diagrama de Coxeter-Dynkin, y seguido del símbolo de Schläfli del politopo semilla regular. Por ejemplo, el octaedro truncado se representa con la notación: t0,1{3,4}.

|
 Triángulos generadores |
| Operación | Símbolo de Schläfli |
Diagrama de Coxeter |
Símbolo de Wythoff |
Posición: | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Original | {p,q} | t0{p,q} | q | 2 p | {p} | {} | -- | -- | -- | {} | ||||
| Birrectificado (o dual) |
{q,p} | t2{p,q} | p | 2 q | -- | {} | {q} | {} | -- | -- | ||||
| Truncado | t{p,q} | t0,1{p,q} | 2 q | p | {2p} | {} | {q} | -- | {} | {} | ||||
| Bitruncado (o dual truncado) |
t{q,p} | t1,2{p,q} | 2 p | q | {p} | {} | {2q} | {} | {} | -- | ||||
| Rectificado | r{p,q} | t1{p,q} | 2 | p q | {p} | -- | {q} | -- | {} | -- | ||||
| Canteado (o expandido) |
rr{p,q} | t0,2{p,q} | p q | 2 | {p} | {}×{} | {q} | {} | -- | {} | ||||
| Cantitruncado (u omnitruncado) |
tr{p,q} | t0,1,2{p,q} | 2 p q | | {2p} | {}×{} | {2q} | {} | {} | {} | ||||
| Operación | Símbolo de Schläfli |
Diagrama de Coxeter |
Símbolo de Wythoff |
Posición: | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Achatado rectificado | sr{p,q} | | 2 p q | {p} | {3} {3} |
{q} | -- | -- | -- | |||||
| Achatado | s{p,2q} | ht0,1{p,q} | s{2p} | {3} | {q} | -- | {3} | ||||||
Cuatro dimensiones
editarEn cuatro dimensiones, hay 6 4-politopos regulares convexos, 17 prismas a partir de los sólidos platónicos y los arquimedianos (excluyendo el cubo-prisma, que ya se ha contado como teseracto) y dos conjuntos infinitos: los prismas a partir de los antiprismas convexos y los duoprismas. También hay 41 4-politopos semirregulares convexos, incluidos la construcción de Wythoff del gran antiprisma y el 24-celdas romo. Ambos 4-politopos especiales están compuestos por subgrupos de los vértices del hexacosicoron.
No se han enumerado todos los politopos estrellados uniformes de cuatro dimensiones. Figuran los 10 4-politopos estrellados regulares (Schläfli-Hess) y los 57 prismas a partir de los poliedros estrellados uniformes, así como tres familias infinitas: los prismas a partir de los antiprismas estrellados, los duoprismas formados a partir del producto cartesiano de dos polígonos estrellados, y los duoprismas, que se forman multiplicando un polígono ordinario por un polígono estrellado. Hay un número desconocido de 4-politopos que no encajan en las categorías anteriores (a comienzos del siglo XXI se habían descubierto más de mil).

Hay 3 ángulos diédricos rectos (2 espejos perpendiculares que se cruzan):
Aristas 1 a 2, 0 a 2 y 1 a 3

Cada politopo regular puede contemplarse como una serie de imágenes de un dominio fundamental reflejado en una pequeña cantidad de espejos. En un politopo de 4 dimensiones (o panal cúbico de 3 dimensiones), la región fundamental está delimitada por cuatro espejos. Un espejo en el 4-espacio es un hiperplano tridimensional, pero para el propósito del artículo es más conveniente considerar solo su intersección bidimensional con la superficie tridimensional de una n-esfera. Por lo tanto, los espejos forman un tetraedro irregular.
Cada uno de los dieciséis 4-politopos regulares es generado por uno de los cuatro grupos de simetría, de la siguiente manera:
- Grupo [3,3,3]: el pentácoron {3,3,3}, que es autodual
- Grupo [3,3,4]: el hexadecacoron {3,3,4} y su dual el teseracto {4,3,3}
- Grupo [3,4,3]: el icositetracoron {3,4,3}, autodual
- Grupo [3,3,5]: el hexacosicoron {3,3,5}, su dual el hecatonicosacoron {5,3,3} y sus diez estelaciones regulares
- Grupo [31,1,1]: contiene solo miembros repetidos de la familia [3,3,4]
(los grupos se muestran con la notación de Coxeter).
Ocho de los panales uniformes convexos en el espacio tridimensional euclídeo se generan de manera análoga a partir del panal cúbico {4,3,4}, aplicando las mismas operaciones utilizadas para generar los 4-politopos uniformes de Wythoff.
Para un simplex de simetría dada, un punto generador se puede colocar en cualquiera de los cuatro vértices, 6 aristas, 4 caras o el volumen interior. Sobre cada uno de estos 15 elementos hay un punto cuyas imágenes, reflejadas en los cuatro espejos, son los vértices de un 4-politopo uniforme.
Los símbolos de Schläfli extendidos están formados por una t seguida de la inclusión de uno a cuatro subíndices 0,1,2,3. Si hay un subíndice, significa que el punto generador está en una esquina de la región fundamental, es decir, un punto donde se encuentran tres espejos. Estas esquinas se anotan como
- 0: vértice del 4-politopo principal (centro de celda del dual)
- 1': centro de arista del original (centro de cara del dual)
- 2: centro de cara del original (centro de arista del dual)
- 3: centro de celda del original (vértice del dual)
(para los dos 4-politopos autoduales, dual significa un 4-politopo semejante en posición dual). Dos o más subíndices significan que el punto generador está entre las esquinas indicadas.
Resumen constructivo
editarA continuación se resumen las 15 formas constructivas por familia. Las familias autoduales se enumeran en una columna, mientras que otras figuran en dos columnas con entradas compartidas del diagrama de Coxeter-Dynkin simétrico. La décima y última fila enumera las construcciones romas del 24-celdas, que incluye todos los 4-politopos uniformes no prismáticos, excepto la construcción de Wythoff del gran antiprisma, que no tiene familia de Coxeter.
| A4 | BC4 | D4 | F4 | H4 | ||
|---|---|---|---|---|---|---|
| [3,3,3] |
[4,3,3] |
[3,31,1] |
[3,4,3] |
[5,3,3] | ||
pentácoron {3,3,3} |
hexadecacoron {3,3,4} |
teseracto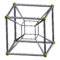 {4,3,3} |
hexadecacoron {3,31,1} |
icositetracoron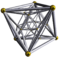 {3,4,3} |
hexacosicoron {3,3,5} |
hecatonicosacoron {5,3,3} |
5-celdas rectificado r{3,3,3} |
16-celdas rectificado r{3,3,4} |
teseracto rectificado r{4,3,3} |
demiteseracto rectificado r{3,31,1} |
24-celdas rectificado r{3,4,3} |
600-celdas rectificado r{3,3,5} |
120-celdas rectificado r{5,3,3} |
5-celdas truncado t{3,3,3} |
16-celdas truncado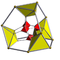 t{3,3,4} |
teseracto truncado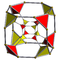 t{4,3,3} |
demiteseracto truncado t{3,31,1} |
24-celdas truncado t{3,4,3} |
600-celdas truncado t{3,3,5} |
120-celdas truncado t{5,3,3} |
5-celdas canteado rr{3,3,3} |
16-celdas canteado rr{3,3,4} |
teseracto canteado rr{4,3,3} |
demiteseracto canteado 2r{3,31,1} |
24-celdas canteado rr{3,4,3} |
600-celdas canteado rr{3,3,5} |
120-celdas canteado rr{5,3,3} |
5-celdas runcinado t0,3{3,3,3} |
16-celdas runcinado t0,3{3,3,4} |
teseracto runcinado t0,3{4,3,3} |
24-celdas runcinado t0,3{3,4,3} |
600-celdas runcinado 120-celdas  t0,3{3,3,5} | ||
5-celdas bitruncado t1,2{3,3,3} |
16-celdas bitruncado 2t{3,3,4} |
teseracto bitruncado 2t{4,3,3} |
demiteseracto cantitruncado 2t{3,31,1} |
24-celdas bitruncado 2t{3,4,3} |
600-celdas bitruncado 120-celdas  2t{3,3,5} | |
5-celdas cantitruncado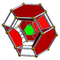 tr{3,3,3} |
16-celdas cantitruncado tr{3,3,4} |
teseracto cantitruncado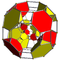 tr{4,3,3} |
demiteseracto omnitruncado tr{3,31,1} |
24-celdas cantitruncado tr{3,4,3} |
600-celdas cantitruncado tr{3,3,5} |
120-celdas cantitruncado tr{5,3,3} |
5-celdas runcitruncado t0,1,3{3,3,3} |
16-celdas runcitruncado t0,1,3{3,3,4} |
teseracto runcitruncado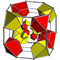 t0,1,3{4,3,3} |
demiteseracto runcicanteado rr{3,31,1} |
24-celdas runcitruncado t0,1,3{3,4,3} |
600-celdas runcitruncado t0,1,3{3,3,5} |
120-celdas runcitruncado t0,1,3{5,3,3} |
5-celdas omnitruncado t0,1,2,3{3,3,3} |
16-celdas omnitruncado t0,1,2,3{3,3,4} |
teseracto omnitruncado t0,1,2,3{3,3,4} |
24-celdas omnitruncado t0,1,2,3{3,4,3} |
120-celdas omnitruncado 600-celdas  t0,1,2,3{5,3,3} | ||
16-celdas cantitruncado alternado sr{3,3,4} |
demiteseracto romo sr{3,31,1} |
24-celdas truncado alternado s{3,4,3} |
||||
Formas truncadas
editarLa siguiente tabla define las 15 formas. Cada forma truncada puede tener de uno a cuatro tipos de celdas, ubicadas en las posiciones 0,1,2,3 como se definió anteriormente. Las celdas están etiquetadas mediante notación de truncamiento poliédrico.
- Un prisma n-gonal se representa como: {n}×{ }.
- El fondo verde se muestra en las formas que son equivalentes a la forma original o su dual.
- El fondo rojo muestra los truncamientos de la forma original y el azul los truncamientos del dual.
| Operación | Símbolo de Schläfli | Diagrama de Coxeter |
Celdas por posición: | ||||
|---|---|---|---|---|---|---|---|
| (3) |
(2) |
(1) |
(0) | ||||
| Original | {p,q,r} | t0{p,q,r} | {p,q} |
-- |
-- |
-- | |
| Rectificado | r{p,q,r} | t1{p,q,r} | r{p,q} |
-- |
-- |
{q,r} | |
| Birrectificado (o dual rectificado) |
2r{p,q,r} = r{r,q,p} |
t2{p,q,r} | {q,p} |
-- |
-- |
r{q,r} | |
| Trirrectificado (o dual) |
3r{p,q,r} = {r,q,p} |
t3{p,q,r} | -- |
-- |
-- |
{r,q} | |
| Truncado | t{p,q,r} | t0,1{p,q,r} | t{p,q} |
-- |
-- |
{q,r} | |
| Bitruncado | 2t{p,q,r} | 2t{p,q,r} | t{q,p} |
-- |
-- |
t{q,r} | |
| Tritruncado (o dual truncado) |
3t{p,q,r} = t{r,q,p} |
t2,3{p,q,r} | {q,p} |
-- |
-- |
t{r,q} | |
| Canteado | rr{p,q,r} | t0,2{p,q,r} | rr{p,q} |
-- |
{}×{r} |
r{q,r} | |
| Bicanteado (o dual canteado) |
r2r{p,q,r} = rr{r,q,p} |
t1,3{p,q,r} | r{p,q} |
{p}×{} |
-- |
rr{q,r} | |
| Runcinado (o expandido) |
e{p,q,r} | t0,3{p,q,r} | {p,q} |
{p}×{} |
{}×{r} |
{r,q} | |
| Cantitruncado | tr{p,q,r} | tr{p,q,r} | tr{p,q} |
-- |
{}×{r} |
t{q,r} | |
| Bicantitruncado (o dual cantitruncado) |
t2r{p,q,r} = tr{r,q,p} |
t1,2,3{p,q,r} | t{q,p} |
{p}×{} |
-- |
tr{q,r} | |
| Runcitruncado | et{p,q,r} | t0,1,3{p,q,r} | t{p,q} |
{2p}×{} |
{}×{r} |
rr{q,r} | |
| Runcicanteado (o dual runcitruncado) |
e3t{p,q,r} = et{r,q,p} |
t0,2,3{p,q,r} | tr{p,q} |
{p}×{} |
{}×{2r} |
t{r,q} | |
| Runcicantitruncado (u omnitruncado) |
o{p,q,r} | t0,1,2,3{p,q,r} | tr{p,q} |
{2p}×{} |
{}×{2r} |
tr{q,r} | |
Formas mitad
editarExisten construcciones mitad, en las que aparecen circunferencias vacías en lugar de nodos anillados. Las ramas vecinas a las circunferencias vacías y a los nodos inactivos deben estar en orden par. Las construcciones mitad siempre presentan disposiciones de vértices idénticas a las de otras construcciones existentes que disponen de nodos anillados.
| Operación | Símbolo de Schläfli | Diagrama de Coxeter |
Celdas por posición: | ||||
|---|---|---|---|---|---|---|---|
| (3) |
(2) |
(1) |
(0) | ||||
| Mitad Alternado |
h{p,2q,r} | ht0{p,2q,r} | h{p,2q} |
-- |
-- |
-- | |
| Rectificado alternado | hr{2p,2q,r} | ht1{2p,2q,r} | hr{2p,2q} |
-- |
-- |
h{2q,r} | |
| Achatado Truncado alternado |
s{p,2q,r} | ht0,1{p,2q,r} | s{p,2q} |
-- |
-- |
h{2q,r} | |
| Biachatado Bitruncamiento alternado |
2s{2p,q,2r} | ht1,2{2p,q,2r} | s{q,2p} |
-- |
-- |
s{q,2r} | |
| Rectificado achatado Rectificado truncado alternado |
sr{p,q,2r} | ht0,1,2{p,q,2r} | sr{p,q} |
-- |
s{2,2r} |
s{q,2r} | |
| Omniachatado Omnitruncado alternado |
os{p,q,r} | ht0,1,2,3{p,q,r} | sr{p,q} |
{p}×{} |
{}×{r} |
sr{q,r} | |
Cinco y más dimensiones
editarEn cinco dimensiones y más, hay 3 politopos regulares, un hipercubo, un símplex y un politopo de cruce, que son generalizaciones del cubo tridimensional, del tetraedro y del octaedro respectivamente. No existen politopos estrellados regulares en estas dimensiones. La mayoría de los politopos uniformes de dimensiones superiores se obtienen modificando los politopos regulares o tomando el producto cartesiano de politopos de dimensiones inferiores.
En seis, siete y ocho dimensiones entran en juego los grupos simples de Lie excepcionales E6, E7 y E8. Al colocar anillos en un número distinto de cero de nodos de los diagramas de Coxeter-Dynkin, se pueden obtener 39 nuevos 6-politopos, 127 nuevos 7-politopos y 255 nuevos 8-politopos. Un ejemplo notable es el 421-politopo.
Panales uniformes
editarRelacionados con el tema de los politopos uniformes finitos están los panales uniformes en espacios euclídeos e hiperbólicos. Los grupos de Coxeter afines generan panales uniformes euclídeos y los grupos de Coxeter hiperbólicos generan panales hiperbólicos. Se pueden multiplicar dos grupos de Coxeter afines.
Hay dos clases de grupos de Coxeter hiperbólicos, los compactos y los paracompactos. Los panales uniformes generados por grupos compactos tienen facetas y figuras de vértices finitas y existen en 2 a 4 dimensiones. Los grupos paracompactos tienen subgrafos afines o hiperbólicos y facetas infinitas o figuras de vértices infinitas, y existen en 2 a 10 dimensiones.
Véase también
editarReferencias
editar- ↑ Mircea Vasile Diudea (2017). Multi-shell Polyhedral Clusters. Springer. pp. 40 de 442. ISBN 9783319641232. Consultado el 22 de agosto de 2023.
Bibliografía
editar- Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins and J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Harold Scott MacDonald Coxeter, Longuet-Higgins, Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401-50. (Extended Schläfli notation used)
- Marco Möller, Vierdimensionale Archimedische Polytope, Dissertation, Universität Hamburg, Hamburg (2004) (en alemán)
Enlaces externos
editar- Olshevsky, George. "Uniform polytope". Glossary for Hyperspace. Archivado desde el original el 4 de febrero de 2007.
- Politopos uniformes y convexos en cuatro dimensiones:, Marco Möller (en alemán)
| Politopos regulares y uniformes convexos fundamentales en las dimensiones 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familia | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Polígono regular | Triángulo | Cuadrado | p-gono | Hexágono | Pentágono | |||||||
| Poliedro uniforme | Tetraedro | Octaedro • Cubo | Demicubo | Dodecaedro • Icosaedro | ||||||||
| 4-politopo uniforme | Pentácoron | Hexadecacoron • Teseracto | Demiteseracto | Icositetracoron | Hecatonicosacoron • Hexacosicoron | |||||||
| 5-politopo uniforme | 5-símplex | 5-ortoplex • Penteracto | 5-demicubo | |||||||||
| 6-politopo uniforme | 6-símplex | 6-ortoplex • Hexeracto | 6-demicubo | 122 • 221 | ||||||||
| 7-politopo uniforme | 7-símplex | 7-ortoplex • Hepteracto | 7-demicubo | 132 • 231 • 321 | ||||||||
| 8-politopo uniforme | 8-símplex | 8-ortoplex • Octoracto | 8-demicubo | 142 • 241 • 421 | ||||||||
| 9-politopo uniforme | 9-símplex | 9-ortoplex • Eneracto | 9-demicubo | |||||||||
| 10-politopo uniforme | 10-símplex | 10-ortoplex • Decaracto | 10-demicubo | |||||||||
| n-politopo uniforme | n-símplex | n-ortoplex • n-cubo | n-demicubo | 1k2 • 2k1 • k21 | n-politopo pentagonal | |||||||
| Relacionados: Familias de politopos • Politopo regular • Anexo:Politopos regulares y compuestos | ||||||||||||













