
Summary
El algoritmo de Kruskal es un algoritmo de la teoría de grafos para encontrar un árbol recubridor mínimo en un grafo conexo y ponderado. Es decir, busca un subconjunto de aristas que, formando un árbol, incluyen todos los vértices y donde el valor de la suma de todas las aristas del árbol es el mínimo. Si el grafo no es conexo, entonces busca un bosque expandido mínimo (un árbol expandido mínimo para cada componente conexa). Este algoritmo toma su nombre de Joseph Kruskal, quien lo publicó por primera vez en 1956.[1] [2] . Otros algoritmos que sirven para hallar el árbol de expansión mínima o árbol recubridor mínimo son el algoritmo de Prim, el algoritmo del borrador inverso y el algoritmo de Boruvka.
Descripción
editarEl algoritmo de Kruskal es un ejemplo de algoritmo voraz que funciona de la siguiente manera:
- se crea un bosque B (un conjunto de árboles), donde cada vértice del grafo es un árbol separado
- se crea un conjunto C que contenga a todas las aristas del grafo
- mientras C es no vacío
- eliminar una arista de peso mínimo de C
- si esa arista conecta dos árboles diferentes se añade al bosque, combinando los dos árboles en un solo árbol
- en caso contrario, se desecha la arista
Al acabar el algoritmo, el bosque tiene un solo componente, el cual forma un árbol de expansión mínimo del grafo.
En un árbol de expansión mínimo se cumple:
- la cantidad de aristas del árbol es la cantidad de nodos menos uno (1).
Pseudocódigo
editar función Kruskal(G)
Para cada v en V[G] hacer
Nuevo conjunto C(v) ← {v}.
Nuevo heap Q que contiene todas las aristas de G, ordenando por su peso
Defino un árbol T ← Ø
// n es el número total de vértices
Mientras T tenga menos de n-1 aristas y !Q.vacío() hacer
(u,v) ← Q.sacarMin()
// previene ciclos en T. agrega (u,v) si u y v están
// diferentes componentes en el conjunto.
// Nótese que C(u) devuelve la componente a la que pertenece u
Si C(v) ≠ C(u) hacer
Agregar arista (v,u) a T
Merge C(v) y C(u) en el conjunto
Responder árbol T
Código en C++
editar#include <vector>
using namespace std;
class Grafo
{
public:
Grafo();
Grafo(int nodos);
vector<vector<int>> kruskal();
private:
const int INF = numeric_limits<int>::max();
int cn; //cantidad de nodos
vector<vector<int>> ady; //matriz de adyacencia
};
//**** Finaliza Archivo grafo.h *****//
//**** Comienza Archivo grafo.cpp *****//
Grafo::Grafo()
{
}
Grafo::Grafo(int nodos)
{
this->cn = nodos;
this->ady = vector<vector<int>>(cn);
for (int i = 0; i < cn; i++)
ady[i] = vector<int>(cn, INF);
}
// Declaraciones en el archivo .h
int cn; //cantidad de nodos
vector< vector<int> > ady; //matriz de adyacencia
// Devuelve la matriz de adyacencia del árbol mínimo.
vector< vector<int> > Grafo :: kruskal(){
vector< vector<int> > adyacencia = this->ady;
vector< vector<int> > arbol(cn);
vector<int> pertenece(cn); // indica a que árbol pertenece el nodo
for(int i = 0; i < cn; i++){
arbol[i] = vector<int> (cn, 0);
pertenece[i] = i;
}
int nodoA;
int nodoB;
int arcos = 1;
while(arcos < cn){
// Encontrar el arco mínimo que no forma ciclo y guardar los nodos y la distancia.
int min = INF;
for(int i = 0; i < cn; i++)
for(int j = 0; j < cn; j++)
if(min > adyacencia[i][j] && adyacencia[i][j]!=0 && pertenece[i] != pertenece[j]){
min = adyacencia[i][j];
nodoA = i;
nodoB = j;
}
// Si los nodos no pertenecen al mismo árbol agrego el arco al árbol mínimo.
if(pertenece[nodoA] != pertenece[nodoB]){
arbol[nodoA][nodoB] = min;
arbol[nodoB][nodoA] = min;
// Todos los nodos del árbol del nodoB ahora pertenecen al árbol del nodoA.
int temp = pertenece[nodoB];
pertenece[nodoB] = pertenece[nodoA];
for(int k = 0; k < cn; k++)
if(pertenece[k] == temp)
pertenece[k] = pertenece[nodoA];
arcos++;
}
}
return arbol;
}
Complejidad del algoritmo
editarm el número de aristas del grafo y n el número de vértices, el algoritmo de Kruskal muestra una complejidad O(m log m) o, equivalentemente, O(m log n), cuando se ejecuta sobre estructuras de datos simples. Los tiempos de ejecución son equivalentes porque:
- m es a lo sumo n2 y log n2 = 2logn es O(log n).
- ignorando los vértices aislados, los cuales forman su propia componente del árbol de expansión mínimo, n ≤ 2m, así que log n es O(log m).
Se puede conseguir esta complejidad de la siguiente manera: primero se ordenan las aristas por su peso usando una ordenación por comparación (comparison sort) con una complejidad del orden de O(m log m); esto permite que el paso "eliminar una arista de peso mínimo de C" se ejecute en tiempo constante. Lo siguiente es usar una estructura de datos para conjuntos disjuntos (disjoint-set data structure) para controlar qué vértices están en qué componentes. Es necesario hacer orden de O(m) operaciones ya que por cada arista hay dos operaciones de búsqueda y posiblemente una unión de conjuntos. Incluso una estructura de datos sobre conjuntos disjuntos simple con uniones por rangos puede ejecutar las operaciones mencionadas en O(m log n). Por tanto, la complejidad total es del orden de O(m log m) = O(m log n).
Con la condición de que las aristas estén ordenadas o puedan ser ordenadas en un tiempo lineal (por ejemplo, mediante el ordenamiento por cuentas o con el ordenamiento Radix), el algoritmo puede usar estructuras de datos de conjuntos disjuntos más complejas para ejecutarse en tiempos del orden de O(m α(n)), donde α es la inversa (tiene un crecimiento extremadamente lento) de la función de Ackermann.
Demostración de la correctitud
editarSea T=[X,A] la gráfica generada por el algoritmo de Kruskal. Por construcción T es acíclica y tiene n-1 aristas; por lo tanto, T es un árbol expandido de G. Ahora se demostrará que T es de costo mínimo.
Sea S=[X,A'] un árbol de costo mínimo de G y supóngase T es distinto de S. Basta probar que S y T tienen el mismo costo para que el algoritmo quede justificado. Para ello se procederá de la siguiente manera:
A partir de los árboles T y S se construirá otro árbol, S1=[X,A´´], de costo mínimo de G con la característica que es más "parecido" a T que S; esto es, si T y S tienen k aristas en común, T y S1 tendrán k+1 aristas en común. Luego si T diferente de S1, a partir de estos dos árboles se construirá otro árbol de costo mínimo, S2, que tendrá k+2 aristas en común con T. Como la cantidad de aristas es finita, el procedimiento propuesto es finito, llegará un momento en que se construirá un árbol Sk de costo mínimo de G que tendrá n-1 aristas en común con T; es decir, se tendrá Sk = T y se podrá concluir que T es un árbol de costo mínimo de G.
Para la construcción del árbol Sr (r=1,2,3, ... ,k), considérese lo siguiente: si T diferente de Sr-1 (So = S) difieren, al menos, en una arista. Sea u1 la arista de menor costo que está en T pero no en Sr-1; es decir C(u1) = min{C(a)}, para toda arista a que pertenece a T tal que a no pertenece a Sr-1. Obsérvese que u1 es la primera arista examinada, durante el algoritmo de Kruskal, que pertenece a T pero no a Sr-1. Por otro lado, como Sr-1 es árbol, existe en él una cadena que une los extremos de u1. Esta cadena contiene una arista u2, que no pertenece a T, puesto que si estuviera toda la cadena se formaría un ciclo con u1 en T. Agréguese u1 a Sr-1 y elíminese u2 de Sr-1. Sea Sr la gráfica resultante y nótese que Sr es un árbol de G.
Ahora solo falta probar que Sr es de costo mínimo. Esto se hará por inducción. Para k=O, se tiene que So = S es un árbol de costo mínimo de G. Supóngase válida la afirmación para k=r-1; esto es, supóngase que Sr-1 es un árbol de costo mínimo de G. Esto implica que: C(Sr-1) <= C(Sr). Y como Sr-1 y Sr difieren sólo en una arista se tiene: C(u2) <= C(u1) ... (I). Basta probar que C(u1) <= (Cu2) para poder conluir que C(Sr-1)=C(Sr). Para esto, supóngase que C(u1) > C(u2) ; nótese que esta suposición implica que la arista u2 fue examinada antes que la arista u1 durante el algoritmo de Kruskal que generó T. Por otro lado, como u2 no fue incluida en T, esta arista forma ciclo con las aristas examinadas antes que ella y que fueron incluidas en T. Sean éstas b1,b2 , ..., bj. Debe observarse que C(bi) <= C(u2) < C(u1) , para i=1,...j; luego, dada la definición de u1, se concluye que b1,b2, ... ,bj pertenecen a Sr-1. Esto es una contradicción, puesto que b1, b2 ,...,bi y u2 formarían ciclo en Sr-1 . Por lo tanto se concluye : C(u1) <= C(u2) ... (II). Y utilizando la expresión (I) y (II) se tiene que: C(u1)=C(u2); por lo tanto, C(Sr-1)=C(Sr), es decir, Sr es un árbol de costo mínimo de G. Nótese que T y Sr contienen ambos a la arista u1 (que no estaba contenida en Sr-1); luego, si T y Sr-1 tienen k aristas en común, T y Sr tienen k+1 aristas en común. Si T = Sr entonces T es de costo mínimo; en caso contrario, constrúyase Sr+1 , del mismo modo que como se construyó Sr a partir de T y Sr . Este procedimiento es finito puesto que el número de aristas de T es finito.
Otros algoritmos para este problema son el algoritmo de Prim y el algoritmo de Boruvka.
Ejemplo
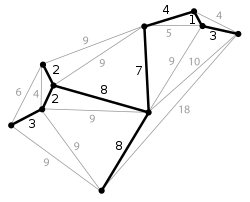
editar| Este es el grafo original. Los números de las aristas indican su peso. Ninguna de las aristas está resaltada. | |
| AD y CE son las aristas más cortas, con peso 5, y AD se ha elegido arbitrariamente, por tanto se resalta. | |
| Sin embargo, ahora es CE la arista más pequeña que no forma ciclos, con peso 5, por lo que se resalta como segunda arista. | |
| La siguiente arista, DF con peso 6, ha sido resaltada utilizando el mismo método. | |
| Las siguientes aristas más pequeñas son AB y BE, ambas con peso 7. AB se elige arbitrariamente, y se resalta. La arista BD se resalta en rojo, porque formaría un ciclo ABD si se hubiera elegido. | |
| El proceso continúa marcando las aristas, BE con peso 7. Muchas otras aristas se marcan en rojo en este paso: BC (formaría el ciclo BCE), DE (formaría el ciclo DEBA), y FE (formaría el ciclo FEBAD). | |
| Finalmente, el proceso termina con la arista EG de peso 9, y se ha encontrado el árbol expandido mínimo con peso total de 39. |
Referencias
editar- ↑ Kruskal, J. B. (1956). «On the shortest spanning subtree and the traveling salesman problem». Proceedings of the American Mathematical Society (7): 48-50. JSTOR 2033241. doi:10.1090/S0002-9939-1956-0078686-7.
- ↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest y Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Sección 23.2: The algorithms of Kruskal and Prim, pp.567–574.
Enlaces externos
editar- Wikilibros alberga un libro o manual sobre Implementación del Algoritmo de Kruskal en Java.
- Animación del algoritmo de Kruskal
- Creación y solución de laberintos por los algoritmos de Kruskal y Prim
- Otra Animación (incluye código en JAVA)
- Implementación del Algoritmo de Kruskal en C++ (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).


