
Summary
En el ámbito de la sismología, las ondas S, ondas secundarias, ondas de cizalla o de corte (a veces denominadas ondas S elásticas) son un tipo de onda elástica, y uno de los dos tipos principales de ondas elásticas internas, denominadas de esta manera ya que se pueden desplazar a través del cuerpo de un objeto, a diferencia de las ondas superficiales.[1]
La onda S se desplaza como una de corte u transversal, de manera que el movimiento es perpendicular a la dirección de propagación de la onda. La onda se desplaza a través de un medio elástico, y la principal fuerza de restitución se debe a efectos de corte.[2] Estas ondas no divergen, y las mismas responden a la ecuación de continuidad para medios incompresibles:
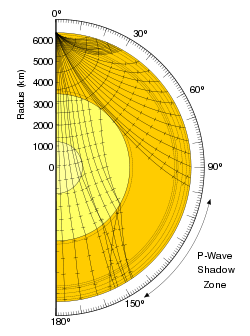
Su nombre, S de secundaria, se debe a que es el segundo tipo de onda directa que se detecta en el sismograma de un terremoto, luego de la onda primaria de compresión, u onda P, porque las ondas S se desplazan a menor velocidad en la roca. A diferencia de la onda P, la onda S no puede desplazarse por el núcleo fundido exterior de la Tierra, y ello produce una zona de sombra de ondas S en el sector opuesto a donde se originaron. Sin embargo las mismas aun pueden ocurrir en el núcleo interior sólido: cuando una onda P impacta la interfase de los núcleos sólido y fundido, las ondas S por lo tanto se propagan en un medio sólido. Y cuando las ondas S impactan la interfase nuevamente las mismas pueden producir ondas P. Esta propiedad le permite a los sismólogos determinar las características del núcleo interior.[3]
Teoría
editarLa teoría analítica de las ondas S se remonta a la década de 1800s.[4] Comenzando con la relación tensión-deformación para un sólido isotrópico utilizando la notación de Einstein:
Donde es la tensión, y son los parámetros de Lamé (con el módulo de cizalladura), es la delta de Kronecker, y se define el tensor de deformaciones
para un desplazamiento de la deformación u. Reemplazando esta segunda expresión en la primera se obtiene:
La segunda ley de Newton en este caso da lugar a la ecuación homogénea de movimiento para la propagación de la onda sísmica:
donde es la densidad. Insertando en la expresión el tensor de tensiones se obtiene:
Aplicando las identidades vectoriales y realizando ciertas aproximaciones se obtiene la ecuación de la onda sísmica en un medio homogéneo:
donde se ha utilizado la notación de Newton para la derivada temporal. Calculando el rotor de esta ecuación y aplicando identidades vectoriales se obtiene:
la cual es la ecuación de onda aplicada al rotor de u con una velocidad que cumple con
Ello describe a la propagación de la onda S. Aplicando la divergencia de la ecuación de la onda sísmica en un medio homogéneo, en vez del rotor, se obtiene la ecuación de propagación de la onda P. Las ondas SH estacionarias se definen mediante la ecuación de Helmholtz
- [5]
donde k es el número de onda.
Véase también
editarReferencias
editar- ↑ What are seismic waves? UPSeis at Michigan Tech
- ↑ S wave US Geological Survey
- ↑ University of Illinois at Chicago (17 de julio de 1997). «Lecture 16 Seismographs and the earth's interior». Archivado desde el original el 7 de mayo de 2002. Consultado el 8 de junio de 2010.
- ↑ En 1830, el matemático francés Siméon Denis Poisson (1781–1840) presentó una teoría de propagación de las ondas elásticas en sólidos: Poisson, S. D. (1831), "Mémoire sur la propagation du mouvement dans les milieux élastiques" (Memoir on the propagation of motion in elastic media), Mémoires de l'Académie des Sciences de l'Institut de France, 10 : 549–605.
.En las pag 595–596 de su memoria, expresa que un terremoto producirá dos tipos de ondas diferentes, una con una velocidad a y la otra con una velocidad b / . From pp. 595–596: "Fácilmente se puede ver que este terremoto dará origen a dos ondas esféricas que se propagaran de manera uniforme, una con velocidad a, y la otra con velocidad b or a / ... )
En la pag 602, Poisson indica que de los tipos de ondas que produce un terremoto, una onda consiste de expansiones y compresiones que se propagan paralelas a la dirección de desplazamiento de la onda, mientras que la otra onda consiste de movimientos de elongación que ocurren en un plano perpendicular a la dirección de desplazamiento de la onda. From p. 602: " … a gran distancia del sitio del terremoto original, y cuando las ondas se han convertido prácticamente en ondas planas en relación a su extensión total, solo subsisten [en el sólido elástico de la Tierra] las velocidades propias de las moléculas, normales o paralelas a dichas superficies; la velocidad normal ocurre en ondas del primer tipo, donde son acompañadas por expansiones que son proporcionales a las mismas, y las velocidades paralelas correspondientes a las ondas del segundo tipo, las cuales no son acompañadas por cambios de volumen, pero si por extensiones y acortamientos lineales.) - ↑ Sheikhhassani, Ramtin (2013). «Scattering of a plane harmonic SH wave by multiple layered inclusions». Wave Motion 51 (3): 517-532. doi:10.1016/j.wavemoti.2013.12.002.
Bibliografía
editar- Shearer, Peter (1999). Introduction to Seismology (1st edición). Cambridge University Press. ISBN 0-521-66023-8.
- Aki, Keiiti; Richards, Paul G. (2002). Quantitative Seismology (2nd edición). University Science Books. ISBN 0-935702-96-2.
- Fowler, C. M. R. (1990). The solid earth. Cambridge, UK: Cambridge University Press. ISBN 0-521-38590-3.
Enlaces externos
editar- Esta obra contiene una traducción derivada de «S-wave» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.





