
Summary
En física, la ley de desplazamiento de Wien es una ley que establece que hay una relación inversa entre la longitud de onda en la que se produce el pico de emisión de un cuerpo negro () y su temperatura ().
Etimología
editarLa ley de desplazamiento de Wien se llama así en honor al físico alemán, Wilhelm Wien.
Historia
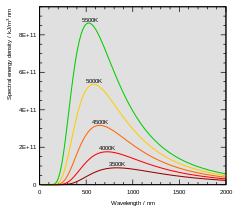
editarWien estudió la distribución de frecuencia o longitud de onda de radiación de cuerpo negro en la década de 1890. Su idea fue utilizar como una buena aproximación para el cuerpo negro ideal un horno con un pequeño orificio. Cualquier radiación que ingrese al pequeño orificio se dispersa y se refleja desde las paredes internas del horno con tanta frecuencia que casi toda la radiación entrante se absorbe y la posibilidad de que parte de ella salga nuevamente del orificio puede hacerse extremadamente pequeña. La radiación que sale de este agujero está entonces muy cerca del equilibrio de la radiación electromagnética del cuerpo negro correspondiente a la temperatura del horno. Wien descubrió que la energía radiactiva ( ) por intervalo de longitud de onda ( ) tiene un máximo a una cierta longitud de onda ( ) y que el máximo se desplaza a longitudes de onda más cortas a medida que aumenta la temperatura ( ). Encontró que el producto ( ) es una constante absoluta: ( 0.2898 cm K).[1]
Introducción
editarLas consecuencias de la ley de Wien es que cuanta mayor sea la temperatura de un cuerpo negro menor es la longitud de onda en la cual emite.
Por ejemplo, la temperatura de la fotosfera solar es de (5780 K) y el pico de emisión se produce a (501,3 nm = 5,013 · 10-7 m). Como 1 angstrom 1 Å= 10-10 m = 10-4 micras resulta que el máximo ocurre a 5013 Å. Como el rango visible se extiende desde 4000 Å hasta 7400 Å, esta longitud de onda cae dentro del espectro visible siendo un tono de verde. Finalmente, el color de la luz que acabamos viendo el sol es blanco y no verde, ya que esta longitud de onda se encuentra en el centro del espectro visible y se mezcla con las demás longitudes que también son de alta intensidad. Es por ello que no vemos al sol irradiar luz verde ni tampoco existen estrellas que irradien en este color. Como complemento, se puede mencionar que la luz blanca del sol solo puede ser apreciada de este color en ausencia de los efectos de la dispersión de la atmósfera, situación tal como una fotografía sacada desde un telescopio espacial o encontrándose en la Estación Espacial Internacional. Desde la superficie terrestre percibimos al Sol de un color amarillento debido a esta dispersión, y varía a medida que la densidad de la atmósfera que se encuentra entre el observador y el objeto celeste también lo hace y esto sucede durante el ciclo natural de rotación de la tierra.
Simbología
editar| Símbolo | Nombre | Valor | Unidad |
|---|---|---|---|
| Temperatura del cuerpo negro | K | ||
| Índice de refracción | |||
| Densidad de Potencia por área por longitud de onda | W / m3 | ||
| Longitud de onda | m | ||
| Longitud de onda del pico de emisión | m | ||
| Constantes | |||
| Constante de desplazamiento de Wien | 0.0028976 | m K | |
| Primera constante de radiación | 3.7418 × 10-16 | W m2 | |
| Segunda constante de radiación | 1.4395 × 107 | nm K | |
| Velocidad de la luz al vacío | 299 792 458 | m / s | |
| Constante de Planck | 6.626 070 15 × 10-34 | J s | |
| Constante de Boltzmann | 1.380649 × 10−23 | J / K |
Descripción
editarMatemáticamente, la ley es:
Con índice de refracción
La ley de Wien fue determinada por su autor en forma empírica, hoy se puede deducir a partir de la ley de Planck para la radiación de un cuerpo negro de la siguiente manera:
| Ley de Planck | |
|---|---|
| Ecuaciones | |
| Ordenando | |
| Derivando | |
| Simplificando | |
| Máximo | |
| Simplificando | |
| Haciendo | |
| Despejando |
Esta ecuación no se puede resolver mediante funciones elementales. Como una solución exacta no es importante podemos optar por soluciones aproximadas. Se puede hallar fácilmente un valor aproximado para :
Si x es grande resulta que aproximadamente así que x está cerca de 5. Así que aproximadamente .
Utilizando el método de Newton o de la tangente:
donde las constantes valen en el Sistema Internacional de Unidades o sistema MKS:
De la definición de x resulta que:
Interpretaciones
editarLa ley de desplazamiento de Wien suele malinterpretarse afirmando que el color de una estrella viene dado por la localización del pico de su curva de Planck. Para que esta interpretación fuese correcta, la cantidad de energía emitida en esa longitud de onda tendría que ser significativamente mayor que en las otras. Pero la variación alrededor del pico es demasiado gradual para que se cumpla esta condición.
La representación de la función de Planck y la expresión de ley de desplazamiento de Wien implican una elección necesaria de variable independiente. En la mayoría de exposiciones, ésta suele ser la longitud de onda. Pero no hay ninguna razón especial para no utilizar otras variables como la frecuencia, el número de onda o el ancho de banda fraccional log(λ) o equivalentemente log(ν).[2] Por ejemplo, en la representación para la frecuencia, el máximo resultante para el espectro solar sería de 880 nm en lugar del 500 nm citado habitualmente para la representación en función de la longitud de onda.
La ley de desplazamiento de Wien no suele utilizarse para determinar la temperatura de una fuente térmica en la práctica aunque se utiliza para predecir aproximadamente la región espectral en la que una fuente térmica irradiará con mayor intensidad. Para obtener un valor numérico, suele ajustarse las mediciones de la intensidad a la temperatura en la función de Planck.[3]
Se han propuesto interpretaciones independientes de la elección de la variables, como la energía media de los fotones emitidos, que para el Sol se correspondería a la longitud de onda de 920 nm[3] o la longitud de onda que divide a la mitad la intensidad total radiada que se correspondería a 710 nm para el espectro solar.[4]
El punto clave sobre la interpretación de la ley de Wien es que la longitud de onda relevante es inversamente proporcional a la temperatura independientemente del criterio elegido para calcularla.
Ejemplos de explicaciones erróneas debido a esta dependencia del máximo con la elección de la variable independiente incluyen la explicación del color del Sol, la evolución del rango espectral del ojo humano y la optimización evolutiva de la fotosíntesis al máximo solar.[5]
Referencias
editar- ↑ https://www.britannica.com/science/Wiens-law
- ↑ Bohren, Craig F.; Clothiaux, Eugene E. (2006-01). Fundamentals of Atmospheric Radiation: An Introduction with 400 Problems (en inglés) (1 edición). Wiley. ISBN 978-3-527-40503-9. doi:10.1002/9783527618620. Consultado el 3 de agosto de 2025.
- ↑ a b Marr, Jonathan M.; Wilkin, Francis P. (1 de mayo de 2012). «A better presentation of Planck’s radiation law». American Journal of Physics 80 (5): 399-405. ISSN 0002-9505. doi:10.1119/1.3696974. Consultado el 3 de agosto de 2025.
- ↑ Heald, Mark A. (1 de diciembre de 2003). «Where is the “Wien peak”?». American Journal of Physics 71 (12): 1322-1323. ISSN 0002-9505. doi:10.1119/1.1604387. Consultado el 3 de agosto de 2025.
- ↑ Soffer, Bernard H.; Lynch, David K. (1 de noviembre de 1999). «Some paradoxes, errors, and resolutions concerning the spectral optimization of human vision». American Journal of Physics 67 (11): 946-953. ISSN 0002-9505. doi:10.1119/1.19170. Consultado el 3 de agosto de 2025.




