
Summary
La lacunaridad (a veces también lagunaridad), del latín lacuna, que significa "hueco" o "laguna", es un término especializado en geometría que se refiere a una medida de cómo los patrones, especialmente los fractales, llenan el espacio, donde los patrones con más o mayores huecos generalmente tienen mayor lacunaridad. Más allá de ser una medida intuitiva de la "huequedad", la lacunaridad puede cuantificar características adicionales de los patrones, como la "invarianza rotacional" y, más generalmente, la heterogeneidad.[1][2][3] Esto se ilustra en la Figura 1, que muestra tres patrones fractales. Cuando se rotan 90°, los dos primeros patrones bastante homogéneos no parecen cambiar, pero la tercera figura más heterogénea sí cambia y tiene correspondientemente una mayor lacunaridad. La primera referencia al término en geometría suele atribuirse a Benoit Mandelbrot, quien en 1983 o quizás tan temprano como 1977 lo introdujo como, en esencia, un complemento al análisis fractal.[4] El análisis de lacunaridad ahora se usa para caracterizar patrones en una amplia variedad de campos y tiene aplicación en el análisis multifractal[5][6] en particular (véase Aplicaciones).
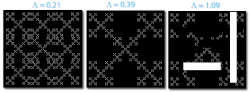

Medición de la lacunaridad
editarEn muchos patrones o conjuntos de datos, la lacunaridad no es fácilmente perceptible o cuantificable, por lo que se han desarrollado métodos asistidos por computadora para calcularla. Como cantidad medible, la lacunaridad a menudo se denota en la literatura científica con las letras griegas o , pero es importante señalar que no hay un estándar único y existen varios métodos diferentes para evaluar e interpretar la lacunaridad.
Contaje por cajas para estimar la lacunaridad
editarUn método conocido para determinar la lacunaridad en patrones extraídos de imágenes digitales utiliza el contaje de cajas, el mismo algoritmo esencial que se usa típicamente para algunos tipos de análisis fractal.[1][4] Similar a mirar una muestra a través de un microscopio con diferentes niveles de aumento, los algoritmos de contaje de cajas examinan una imagen digital desde muchos niveles de resolución para ver cómo ciertas características cambian con el tamaño del elemento utilizado para inspeccionar la imagen. Básicamente, la disposición de píxeles se mide usando elementos tradicionalmente cuadrados (es decir, en forma de caja) de un conjunto arbitrario de tamaños , convencionalmente denotados como s. Para cada , una caja de tamaño se coloca sucesivamente sobre la imagen, cubriéndola completamente al final, y cada vez que se coloca, se registra el número de píxeles que caen dentro de la caja.[nota 1] En el contaje de cajas estándar, la caja para cada en se coloca como si fuera parte de una cuadrícula superpuesta sobre la imagen, de modo que la caja no se superponga a sí misma, pero en los algoritmos de caja deslizante, la caja se desliza sobre la imagen superponiéndose a sí misma y se calcula la "Lacunaridad de Caja Deslizante" o SLac.[3] La Figura 2 ilustra ambos tipos de contaje de cajas.
Cálculos a partir del contaje por cajas
editarLos datos recopilados para cada se manipulan para calcular la lacunaridad. Una medida, denotada aquí como , se obtiene a partir del coeficiente de variación ( ), calculado como la desviación estándar ( ) dividida por la media ( ), para píxeles por caja.[1][3][6] Debido a que la forma en que se muestrea una imagen dependerá de la ubicación inicial arbitraria, para cualquier imagen muestreada en cualquier , habrá un número ( ) de orientaciones posibles, cada una denotada aquí por , sobre las que se pueden recopilar los datos, lo que puede tener efectos variables en la distribución medida de píxeles.[5][nota 2] La ecuación 1 muestra el método básico para calcular :
|
|
(1) |
Distribuciones de probabilidad
editarAlternativamente, algunos métodos ordenan los números de píxeles contados en una distribución de probabilidad con intervalos, y usan los tamaños de los intervalos (masas, ) y sus probabilidades correspondientes ( ) para calcular según las ecuaciones 2 a 5:
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
Interpretación de λ
editarLa lacunaridad basada en se ha evaluado de varias formas, incluyendo el uso de la variación o el valor promedio de para cada (ver Ecuación 6) y mediante la variación o promedio en todas las cuadrículas (ver Ecuación 7).[1][5][7][8]
|
|
(6) |
|
|
(7) |
Relación con la dimensión fractal
editarLos análisis de lacunaridad que utilizan los tipos de valores mencionados han demostrado que los conjuntos de datos extraídos de fractales densos, de patrones que cambian poco al rotarse o de patrones homogéneos tienen baja lacunaridad, pero a medida que estas características aumentan,[cita requerida] generalmente también lo hace la lacunaridad. En algunos casos, se ha demostrado que las dimensiones fractales y los valores de lacunaridad estaban correlacionados,[1] pero investigaciones más recientes indican que esta relación no se cumple para todos los tipos de patrones y medidas de lacunaridad.[5] De hecho, como propuso originalmente Mandelbrot, se ha comprobado que la lacunaridad es útil para distinguir entre patrones (por ejemplo, fractales, texturas, etc.) que comparten o tienen dimensiones fractales similares en diversos campos científicos, incluyendo la neurociencia.[8]
Lacunaridad gráfica
editarOtros métodos para evaluar la lacunaridad a partir de datos de contaje de cajas utilizan la relación entre los valores de lacunaridad (por ejemplo, ) y de maneras distintas a las mencionadas. Un método analiza la gráfica de versus de estos valores. Según este método, la curva puede analizarse visualmente o la pendiente en puede calcularse a partir de la línea de regresión del gráfico .[2] Dado que tienden a comportarse de ciertas formas para patrones mono-, multi- y no fractales, las gráficas de lacunaridad se han utilizado para complementar métodos de clasificación de dichos patrones.[5][8]
Para realizar estas gráficas, los datos del contaje de cajas primero deben transformarse como en la Ecuación 9:
|
|
(9) |
Esta transformación evita valores indefinidos, lo cual es importante porque imágenes homogéneas tendrán en algún igual a 0, haciendo imposible encontrar la pendiente de la línea de regresión de versus . Con , las imágenes homogéneas tienen una pendiente de 0, lo que intuitivamente corresponde a la idea de ausencia de invariancia rotacional o traslacional y de huecos.[9]
Una técnica de contaje de cajas que utiliza una caja "deslizante" calcula la lacunaridad según:
|
|
(10) |
es el número de puntos de datos llenos en la caja y la distribución de frecuencia normalizada de para diferentes tamaños de caja.
Lacunaridad del prefactor
editarOtra forma propuesta de evaluar la lacunaridad mediante contaje de cajas, el método del Prefactor, se basa en el valor obtenido del contaje de cajas para la dimensión fractal ( ). Esta estadística utiliza la variable de la regla de escalado , donde se calcula a partir de la intersección en de la línea de regresión ln-ln para y el conteo ( ) de cajas que tenían al menos un píxel o bien en . se ve particularmente afectada por el tamaño de la imagen y la forma en que se recopilan los datos, especialmente por el límite inferior de utilizado. La medida final se calcula como se muestra en las Ecuaciones 11 a 13:[1][4]
|
|
(11) |
|
|
(12) |
|
|
(13) |
Aplicaciones
editarA continuación, se presenta una lista de algunos campos donde la lacunaridad juega un papel importante, junto con enlaces a investigaciones relevantes que ilustran usos prácticos de la lacunaridad.
- Ecología[2]
- Física[10]
- Arqueología[11]
- Imágenes médicas[6][12]
- Análisis espacial urbano[13][14]
- Estudios sísmicos[15]
- Odontología[16]
- Ciencia de los alimentos[17]
Notas
editar- ↑ Esto contrasta con el contaje de cajas en el análisis fractal, donde se cuenta el número total de cajas que contienen cualquier píxel para determinar una dimensión fractal.
- ↑ Ver FracLac,, contaje de Cajas para una explicación de los métodos para abordar la variación con la ubicación de la cuadrícula
Referencias
editar- ↑ a b c d e f Smith, T. G.; Lange, G. D.; Marks, W. B. (1996). «Fractal methods and results in cellular morphology — dimensions, lacunarity and multifractals». Journal of Neuroscience Methods 69 (2): 123-136. PMID 8946315. S2CID 20175299. doi:10.1016/S0165-0270(96)00080-5.
- ↑ a b c Plotnick, R. E.; Gardner, R. H.; W. W.; K.; M. (1996). «Lacunarity analysis: A general technique for the analysis of spatial patterns». Physical Review E 53 (5): 5461-8. Bibcode:1996PhRvE..53.5461P. PMID 9964879. doi:10.1103/physreve.53.5461.
- ↑ a b c Plotnick, R. E.; Gardner, R. H.; O'Neill, R. V. (1993). «Lacunarity indices as measures of landscape texture». Landscape Ecology 8 (3): 201. S2CID 7112365. doi:10.1007/BF00125351.
- ↑ a b c Mandelbrot, Benoit (1983). The Fractal Geometry of Nature. ISBN 978-0-7167-1186-5.
- ↑ a b c d e Karperien (2004). «Chapter 8 Multifractality and Lacunarity». Defining Microglial Morphology: Form, Function, and Fractal Dimension. Charles Sturt University. Archivado desde el original
|urlarchivo=requiere|url=(ayuda) el 3 de marzo de 2016. Consultado el 22 de julio de 2025. - ↑ a b c Al-Kadi, O.S.; Watson, D. (2008). «Texture Analysis of Aggressive and non-Aggressive Lung Tumor CE CT Images». IEEE Transactions on Biomedical Engineering 55 (7): 1822-30. PMID 18595800. S2CID 14784161. doi:10.1109/TBME.2008.919735. Archivado desde el original el 13 de abril de 2014. Consultado el 10 de abril de 2014.
- ↑ McIntyre, N. E.; Wiens, J. A. (2000). «A novel use of the lacunarity index to discern landscape function». Landscape Ecology 15 (4): 313. S2CID 18644861. doi:10.1023/A:1008148514268.
- ↑ a b c Jelinek, Herbert; Karperien, Audrey; Milosevic, Nebojsa (June 2011). «Lacunarity Analysis and Classification of Microglia in Neuroscience». 8th European Conference on Mathematical and Theoretical Biology, Kraków.
- ↑ Karperien (2002). «Interpreting Lacunarity». FracLac. Archivado desde el original el 20 de septiembre de 2008.
- ↑ Tolle, C. (2003). «Lacunarity definition for ramified data sets based on optimal cover». Physica D: Nonlinear Phenomena 179 (3–4): 129-201. Bibcode:2003PhyD..179..129T. doi:10.1016/S0167-2789(03)00029-0.
- ↑ Stevens, N. E.; Harro, D. R.; Hicklin, A. (2010). «Practical quantitative lithic use-wear analysis using multiple classifiers». Journal of Archaeological Science 37 (10): 2671. doi:10.1016/j.jas.2010.06.004.
- ↑ Rievra-Virtudazo, R.V.; Tapia, A.K.G; Valenzuela, J.F.B.; Cruz, L.D.; Mendoza, H.D.; Castriciones, E.V. (23 de noviembre de 2008). «47. Lacunarity analysis of TEM Images of Heat-Treated Hybrid Organosilica Materials». En Sener, Bilge, ed. Innovations in Chemical Biology. Springer. pp. 397-404. ISBN 978-1-4020-6955-0.
- ↑ Filho, M.B.; Sobreira, F. (2008). «Accuracy of Lacunarity Algorithms in Texture Classification of High Spatial Resolution Images from Urban Areas». The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences XXXVII (Part B3b).
- ↑ Gorsich, D. J.; Tolle, C. R.; Karlsen, R. E.; Gerhart, G. R. (1996). «Wavelet and fractal analysis of ground-vehicle images». En Unser, Michael A; Aldroubi, Akram; Laine, Andrew F, eds. Wavelet Applications in Signal and Image Processing IV. Wavelet Applications in Signal and Image Processing IV 2825. pp. 109-119. S2CID 121560110. doi:10.1117/12.255224.
- ↑ Vannucchi, P.; Leoni, L. (30 de octubre de 2007). «Structural characterization of the Costa Rica decollement: Evidence for seismically-induced fluid pulsing». Earth and Planetary Science Letters 262 (3–4): 413-428. Bibcode:2007E&PSL.262..413V. doi:10.1016/j.epsl.2007.07.056. hdl:2158/257208.
- ↑ Yaşar, F.; Akgünlü, F. (2005). «Fractal dimension and lacunarity analysis of dental radiographs». Dentomaxillofacial Radiology 34 (5): 261-267. PMID 16120874. doi:10.1259/dmfr/85149245.
- ↑ Valous, N.A.; Sun, D.-W.; Allen, P.; Mendoza, F. (January 2010). «The use of lacunarity for visual texture characterization of pre-sliced cooked pork ham surface intensities». Food Research International 43 (1): 387-395. doi:10.1016/j.foodres.2009.10.018.


